OSgL (general)

OSgL (general) contains definitions of general elements and data types used by all other OSxL schemas. Thus OSgL is usually included in the beginning of another OSxL schema through the statement:

<xs:include schemaLocation="OSgL.xsd"/>

For example, the following figure shows the <intVector> data type in OSgL that is used in OSiL for defining a vector of row or column indexes.

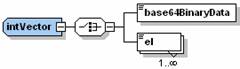
<xs:complexType name="intVector">
       <xs:choice>
             <xs:element name="base64BinaryData" type="base64BinaryData"/>
             <xs:element name="el" maxOccurs="unbounded">
                    <xs:complexType>
                           <xs:simpleContent>
                                 <xs:extension base="xs: int ">
                                        <xs:attribute name="mult" type="xs:positiveInteger" use="optional" default="1"/>
                                        <xs:attribute name="incr" type="xs:int" use="optional" default="0"/>
                                 </xs:extension>
                           </xs:simpleContent>
                    </xs:complexType>
             </xs:element>
       </xs:choice>
</xs:complexType>

An <intVector> may have one or more <el> children or a <base64BinaryData> child if the data in the <el> elements are compressed. The compression is explained in detail in the LPFML paper. Each <el> element has a mult attribute (for multiplicity) with a default value 1 and an incr attribute (for increment) with a default value 0. For example

and

is more concisely expressed as

There is also a similar <doubleVector> data type defined in OSgL.

In the following table, we list some common data types defined in OSgL.

Type Name	Brief Description
intVector	vector of integers
doubleVector	vector of doubles
elType	el element with a name and a value attribute and a description text
mapType	a sequence of el elements (name-value pairs)
base64Binary	compression of a sequence of data usually expressed in el elements; see the LPFML paper [53]
sparseVector	sparse vector with an idx array and a nonz value array
listMatrix	typical sparse matrix storage type with a start array, a choice of rowIdx or colIdx array, and a nonzero value array
mpsMatrix	MPS style sparse matrix storage with a sequence of col (or row) elements; each col (or row) element is in turn a sequence of row (or col) elements
matrixMarket	common sparse matrix storage used in linear algebra with a sequence of el elements; each element is a double value (for a matrix entry) with a row and a col attribute (for matrix indexes)
xmlData	a sequence of any data

In The following table, we list typical function-related elements. Many of these functions are distribution functions. All the distribution functions can have an optional cdf boolean attribute which is false by default. If true, the distribution function is a cumulative distribution function. If false, the distribution is a probability distribution function (pdf, for continuous distributions) or probability mass function (pmf, for discrete distributions). Many of these functions have parameters which are expressed as element attributes. The distribution functions are widely used in the OSiL extension to stochastic programming.

Function Name	Brief Description
userFunctions	a sequence of userFunction elements; each userFunction element contains one OSnLNode as an expression tree root for expressing a function
userVariables	a sequence of userVariable elements; each userVariable element contains one OSnLNode as an expression tree root for expressing a user defined variable
discreteUniform	Discrete Uniform function with a parameter N
bernoulli	Bernoulli function with a parameter p
binomial	Binomial function with parameters N, p
hypergeometric	Hypergeometric function with parameters N, M, n
poisson	Poisson function with a parameter lamda
geometric	Geometric function with a parameter p
negativeBinomial	Negative Binomial function with a parameter p, r
empiricalDiscrete	Empirical Discrete function with a sequence of el elements; each el element is a double value and has a prob attribute
empiricalContinuous	Empirical Continuous function with a sequence of el elements; each el element contains one OSnLNode as an expression tree root for expressing a function and a from and a to attribute for the function domain
uniform	Uniform function with parameters a, b
normal	Normal function with parameters mu, sigma
stdNormal	Standard normal function
exponential	Exponential function with a parameter lamda
weibull	Weibull function with parameters location, scale, shape
erlang	Erlang function with parameters lamda, n
gamma	Gamma function with parameters location, scale, shape
beta	Beta function with parameters degree1, degree2
betaGeneral	General Beta function with parameters degree1, degree2, min, max
lognormal	Lognormal function with parameters mu, sigma
cauchy	Cauchy function with parameters location, scale
t	Student T function with a parameter degree
chiSquare	Chi Square function with a parameter degree
f	F function with parameters degree1, degree2
logistic	Logistic function with parameters mu and beta
logLogistic	Log Logistic function with parameters mu and beta
logarithmic	Logarithmic function with parameters a, b
pareto	Pareto function with parameters shape and scale
rayleigh	Rayleigh function with a parameter beta
pert	Pert function with parameters a, c, b
triangular	Triangular function with parameters a, c, b
multivariateDiscrete	Multivariate Discrete function with a sequence of 2 or more scenario elements; each scenario is a sequence of 2 or more el elements of double values
multinomial	Multinomial function with a parameter N and a sequence of el elements of probability values
bivariateNormal	Bivariate Normal function with parameters mu1, sigma1, mu2, sigma2, rho
multivariateNormal	Multivariate Normal function with a sequence of 3 or more mu elements and a covariance matrix of matrixMarket type
linearTransformation	Linear transformation function with a numberRows and a numberColumns attribute; it contains one constants element of type doubleVector, one matrix element of type matrixMarket, and a randomVariables element to indicate a multivariate distribution

Elements of similar types can be grouped and referenced together. For example the discreteDistributionGroup group shown in the following figure is used to group all the discrete distribution functions in the above table.

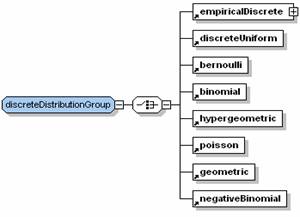
<xs:group name="discreteDistributionGroup">
       <xs:choice>
             <xs:element ref="empiricalDiscrete"/>
             <xs:element ref="discreteUniform"/>
             <xs:element ref="bernoulli"/>
             <xs:element ref="binomial"/>
             <xs:element ref="hypergeometric"/>
             <xs:element ref="poisson"/>
             <xs:element ref="geometric"/>
             <xs:element ref="negativeBinomial"/>
       </xs:choice>
</xs:group>

A continuousDistributionGroup is similarly defined. The more general distributionGroup is a group of discreteDistributionGroup and continuousDistributionGroup as shown in the following figure.

<xs:group name="distributionGroup">
       <xs:choice>
             <xs:group ref="discreteDistributionGroup"/>
             <xs:group ref="continuousDistributionGroup"/>
       </xs:choice>
</xs:group>

Links:

Click to see or download the OSgL XML Schema -> OSgL.xsd




	© Optimization Services (OS) 2006 \| All rights reserved.