|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
| void CppAD::local::reverse_sweep | ( | size_t | d, |
| size_t | n, | ||
| size_t | numvar, | ||
| const local::player< Base > * | play, | ||
| size_t | J, | ||
| const Base * | Taylor, | ||
| size_t | K, | ||
| Base * | Partial, | ||
| bool * | cskip_op, | ||
| const pod_vector< addr_t > & | var_by_load_op, | ||
| const pod_vector< addr_t > & | subgraph | ||
| ) |
Compute derivative of arbitrary order forward mode Taylor coefficients.
| Base | this operation sequence was recorded using AD<Base> and computations by this routine are done using type Base. |
| d | is the highest order Taylor coefficients that we are computing the derivative of. |
| n | is the number of independent variables on the tape. |
| numvar | is the total number of variables on the tape. This is also equal to the number of rows in the matrix Taylor; i.e., play->num_var_rec(). |
| play | The information stored in play is a recording of the operations corresponding to the function
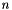 is the number of independent variables and is the number of independent variables and 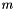 is the number of dependent variables. We define is the number of dependent variables. We define 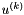 as the value of as the value of x_k in the previous call of the form f.Forward(k, x_k) We define 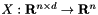 by by
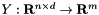 by by
 by by
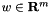 , is defined below under the heading Partial.) Note that the scale factor 1 / k converts the k-th partial derivative to the k-th order Taylor coefficient. This routine computes the derivative of , is defined below under the heading Partial.) Note that the scale factor 1 / k converts the k-th partial derivative to the k-th order Taylor coefficient. This routine computes the derivative of 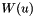 with respect to all the Taylor coefficients with respect to all the Taylor coefficients 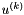 for for 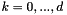 . . |
| J | Is the number of columns in the coefficient matrix Taylor. This must be greater than or equal d + 1. |
| Taylor | For i = 1 , ... , numvar, and for k = 0 , ... , d, Taylor [ i * J + k ] is the k-th order Taylor coefficient corresponding to variable with index i on the tape. The value 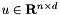 , at which the derivative is computed, is defined by , at which the derivative is computed, is defined by 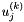 = Taylor [ j * J + k ] for j = 1 , ... , n, and for k = 0 , ... , d. = Taylor [ j * J + k ] for j = 1 , ... , n, and for k = 0 , ... , d. |
| K | Is the number of columns in the partial derivative matrix Partial. It must be greater than or equal d + 1. |
| Partial | Input: The last 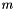 rows of Partial are inputs. The matrix rows of Partial are inputs. The matrix 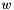 , used to define , used to define 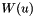 , is specified by these rows. For i = 0 , ... , m - 1, for k = 0 , ... , d, , is specified by these rows. For i = 0 , ... , m - 1, for k = 0 , ... , d, Partial [ (numvar - m + i ) * K + k ] = w[i,k]. Temporary: For i = n+1 , ... , numvar - 1 and for k = 0 , ... , d, the value of Partial [ i * K + k ] is used for temporary work space and its output value is not defined. Output: For j = 1 , ... , n and for k = 0 , ... , d, Partial [ j * K + k ] is the partial derivative of 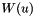 with respect to with respect to 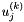 . . |
| cskip_op | Is a vector with size play->num_op_rec(). If cskip_op[i] is true, the operator index i in the recording does not affect any of the dependent variable (given the value of the independent variables). Note that all the operators in an atomic function call are skipped as a block, so only the last UserOp fore each call needs to have cskip_op[i] true. |
| var_by_load_op | is a vector with size play->num_load_op_rec(). It contains the variable index corresponding to each load instruction. In the case where the index is zero, the instruction corresponds to a parameter (not variable). |
| subgraph | is the set of operators over which the reverse mode calculations will be preformed. For k = 0, ... , subgraph.size() - 1, subgraph[k] is an operator index and play->num_op_rec() > subgraph[k] > subgraph[k-1]
|
Definition at line 183 of file reverse_sweep.hpp.
Referenced by CppAD::ADFun< Base >::Reverse(), and CppAD::ADFun< Base >::subgraph_reverse().