|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
| void CppAD::ADFun< Base >::subgraph_reverse | ( | size_t | q, |
| size_t | ell, | ||
| SizeVector & | col, | ||
| VectorBase & | dw | ||
| ) |
Use reverse mode to compute derivative of Taylor coefficients on a subgraph.
The function 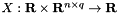 is defined by
is defined by
![\[ X(t , u) = \sum_{k=0}^{q-1} u^{(k)} t^k \]](form_46.png)
The function 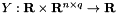 is defined by
is defined by
![\[ Y(t , u) = F[ X(t, u) ] \]](form_48.png)
The function 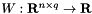 is defined by
is defined by
![\[ W(u) = \sum_{k=0}^{q-1} ( w^{(k)} )^{\rm T} \frac{1}{k !} \frac{ \partial^k } { t^k } Y(0, u) \]](form_50.png)
| q | is the number of Taylor coefficient we are differentiating. |
| ell | is the component of the range that is selected for differentiation. |
| col | is the set of indices j = col[c] where the return value is defined. If an index j is not in col, then either its derivative is zero, or it is not in select_domain. |
| dw | Is a vector 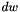 such that for j = col[c], such that for j = col[c], 
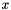 is the value for is the value for 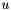 that corresponding to the forward mode Taylor coefficients for the independent variables as specified by previous calls to Forward. that corresponding to the forward mode Taylor coefficients for the independent variables as specified by previous calls to Forward. |
Definition at line 259 of file subgraph_reverse.hpp.