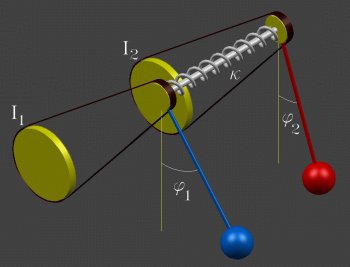
There are other physical analogues, including a pair of current driven Josephsen point junctions.
There are no simple periodic motions (because of the damping), but periodic motions of the second kind, in which both pendula travel at least once around the axle do exist. They satisfy the two point boundary value problem --
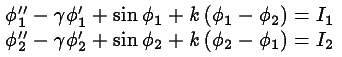
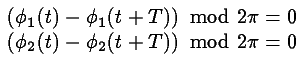
These motions were computed using multifario. Each point on the surface below (T on the vertical axis and the sum and difference of the two torques on the horizontal) is a periodic motion. The damping g=.5, and spring constant k=.1 are fixed. The surface is periodic in the half difference of the two torques (width kp). The surface is displayed over three fundemental strips, and sheets crossing the strip edge have been chosen to give a smooth surface.
Two "points" on this surface, with period T=50 are shown below. The
position of each pendulum is shown over time, in something like a multiple
exposure photograph (I find this is either obvious, or inexplicable).
| (I1+I2)/2 = .676, (I2-I1)/2 = .300 kp | (I1+I2)/2 = .734, (I2-I1)/2 = .525 kp |