Multifario - Computing Stationary Points of Clamped Elastica

This is joint work with Sebastien Neukirch, EPFL.

Neukirch, Sebastien, and Henderson,. Michael E., "Classification of the spatial equilibria of the clamped elastica: symmetries and zoology of solutions", to appear Journal of Elasticity

          Henderson,. Michael E. and Neukirch, Sebastien, "Classification of the spatial equilibria of the clamped elastica", to appear, IJBC.

The physical situation is something like this:

It is also a model (in some sense) for folding in DNA.

The equations for a stationary configuration of the clamped elastica are:

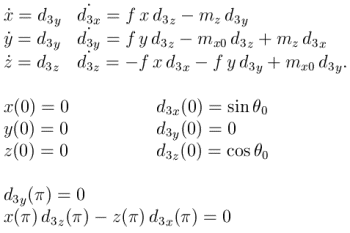
There are three parameters, f - the force applied at the ends (along the z-axis), and the two moments mx0 and mz. A careful counting shows that there are two degrees of freedom, and the solutions lie on a surface.

After discretization, these configurations were computed using multifario. Each point on the surface below (the applid force f  thehorizontal axis and the two components of the applied moment mx0 and mz the vertical) is a configuration of the rod. There are symmetries about the coordinate planes, so one octant gives the whole picture (left). There are more sheets, we restricted ourselves to wave numbers less than five. The figure on the right shows the rods that are "nearly" closed rings (and four octants are shown).

This surface is pretty difficult to understand. The colors are a way to dissect the surface into pieces based on topological numbers similar to winding numbers. If we look only for closed rings (1 extra condition), we have curves of stationary configurations. These are shown below
 

	1	2
"Plus"
"Minus"
	3	4
"Plus"
"Minus"

Below are some solutions on these surfaces. The top left shows the transition from the doubly covered planar ring to the singly covered ring.