Multifario - Overview of the Algorithm

This is a quick overview of the algorithm used in multifario.A detailed version is in the paper

Henderson, Michael E., "Multiple Parameter Continuation: Computing Implicitly Defined k-manifolds", IJBC v12(3), pages 451-76.

First, multifario is a "Continuation Method", sometimes called "Numerical Continuation". Nonlinear problems are difficult to solve globally (i.e. all solutions). Locally things are much better, and for many classes of nonlinear problems a local approximation to the solution can be found. Continuation Methods attempt to build a global solution by piecing together these local approximations. They start with a "known" solution, and by finding iteratively finding solutions near a known point, cover a "component" (all solutions connected to the known solution).

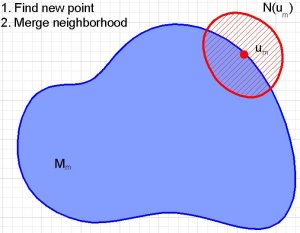
If we have a set of points and local approximations (which cover a small piece of the manifold near the point) it is clear that the next point should be near the boundary of the union of the part of the manifold covered by all the approximations. This way roughly half of the new approximation covers manifold that was not previously known.

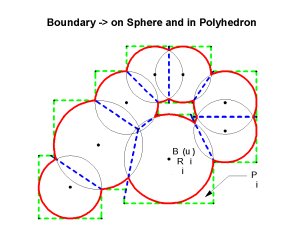
So how do we find a point on the boundary of a union of neighborhoods of points on a manifold? It doesn't sound easy, but if the neighborhoods are the projection of spherical balls in the tangent space at the point, there is an easily implemented algorithm for finding such a point. Here is a sketch of the boundary of a union:

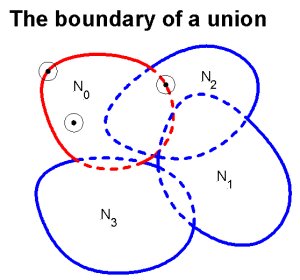
Any point that is not on the boundary of one of the neighborhoods must be interior to the union. This breaks the boundary of the union up into pieces depending on which boundary it lies on. The part of the boundary of N0, for example, which lies on the boundary of the union is the part that is not interior to any of the other neighborhoods. We might start with the boundary of N0, and subtract off the part which is in N1, N2, and N3 and end up with the part that lies on the boundary.

While this can be done in 2d for neighborhoods whose boundaries are single curves, in higher dimensions it is not feasible. So lets look at the subtractions, and do them pairwise, and intersect the results:

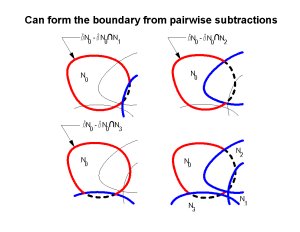
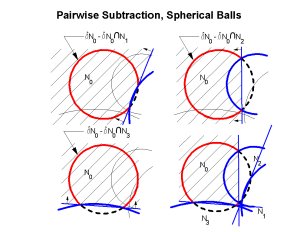
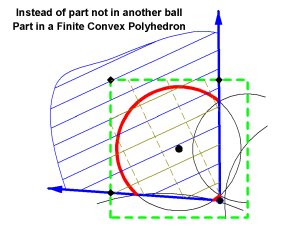
This is a set identity, but how does it help? Well, if the blobs are spherical balls (remember, this is just a sketch, we're working in k-dimensional space here!) these pairwise intersections are simple. Because of the high degree of symmetry, the part of a sphere that lies outside a spherical ball is the part in the halfspace on one side of a plane. The plane is orthogonal to the line between the centers of the two balls, and it's position as a fraction of the distance between the balls is a simple expression involving the ratio of the radii of the balls.

So, now all we have to do is find the part of the sphere in the polyhedron formed by intersecting these half spaces (this works in any dimension!). And, since the polyhedron outside the ball is immaterial to the result, we can start with a cube containing the ball and subtract half spaces to get a convex, finite polyhedron, and the part of the sphere which lies inside this polyhedron is the part that is on the boundary of the union.

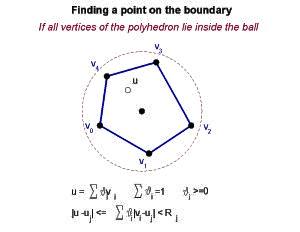
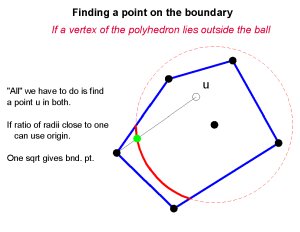
Now, this is actually a well known object. The intersection of the set of polyhedra with the interior of the balls is part of the Laguerre Voronoi diagram of the balls, and there are many nice results about it and it's dual.

But how do we find a point on the boundary? Well, it depends on the vertices of the polyhedron. If all the vertices are inside the ball the intersection with the sphere is empty, and there is no part on the boundary. If one vertex is outside the ball, and we can find one point inside a line between the two crosses the sphere at a point that is on the boundary. And if the ratio of the radii of adjacent balls is between sqrt(2) and 1/sqrt(2) the center of the ball is inside the polyhedron, so this is a simple operation.

OK, but this is for flat "surfaces". Not very interesting (well, I find it interesting. Go stare at the animation:) If the balls are small enough relative to the curvature of the manifold the flat surface picture is pretty close to being right, and we can find the polyhedron by projecting all the adjacent balls into the tangent space the polyhedron lives in.

There is a small error involved, but since we only need a point near the boundary, a point a small distance interior is not a problem. However, there may also be small pieces of boundary left over that we think are covered (i.e. two points may be just a little further apart than the sum of their radii). This isn't too terribly bad either, and can be checked easily and a ball added if it bothers you.

There. That's it. The manifold is represented by a list of points. Each has a tangent space, a ball (just a radius), and a polyhedron (begins as a cube slightly larger than the ball).

To find a point near the boundary we find a polyhedron with a vertex outside it's ball (keep a list of such balls, and take the first off the list - new balls get added to the list, when the first ball has no such vertices remove it from the list). The new point is actually in the tangent space of the manifold, and somehow must be projected onto the manifold.
To add a new ball, add the ball/polyhedron to the list, and to the list of balls that may have a boundary. Then find all the nearby balls (using hierarchical bounding boxes make this a log(m) operation), and for each project the center into the tangent space of the new ball and subtract a half space (and vice versa).

The only "hard" part is finding a point on the manifold, it's tangent plane, and an estimate for the curvature (to get the radius). For implicitly defined manifold this is "easy". Newton's method can be used to project orthogonal to the tangent space onto the manifold. The tangent space is the null space of the Jacobian, and the radius can be estimated by the distance between the point from Newton's method and the tangent plane, and from the number of Newton steps needed.

[Comments | Multifario home page ]