pulp: Pulp classes¶
| LpProblem | |
| LpVariable | |
| LpAffineExpression | |
| LpConstraint | |
| LpConstraint.makeElasticSubProblem | |
| FixedElasticSubProblem |
Todo
LpFractionConstraint, FractionElasticSubProblem
The LpProblem Class¶
- class pulp.LpProblem(name='NoName', sense=1)¶
Bases: object
An LP Problem
Creates an LP Problem
This function creates a new LP Problem with the specified associated parameters
Parameters: - name – name of the problem used in the output .lp file
- sense – of the LP problem objective. Either LpMinimize (default) or LpMaximize.
Returns: An LP Problem
Three important attributes of the problem are:
- objective¶
- The objective of the problem, an LpAffineExpression
- constraints¶
- An ordered dictionary of constraints of the problem - indexed by their names.
Some of the more important methods:
- solve(solver=None, **kwargs)¶
Solve the given Lp problem.
This function changes the problem to make it suitable for solving then calls the solver.actualSolve method to find the solution
Parameter: solver – Optional: the specific solver to be used, defaults to the default solver. - Side Effects:
- The attributes of the problem object are changed in actualSolve() to reflect the Lp solution
- roundSolution(epsInt=1.0000000000000001e-05, eps=9.9999999999999995e-08)¶
Rounds the lp variables
- Inputs:
- none
- Side Effects:
- The lp variables are rounded
- setObjective(obj)¶
Sets the input variable as the objective function. Used in Columnwise Modelling
Parameter: obj – the objective function of type LpConstraintVar - Side Effects:
- The objective function is set
- writeLP(filename, writeSOS=1, mip=1)¶
Write the given Lp problem to a .lp file.
This function writes the specifications (objective function, constraints, variables) of the defined Lp problem to a file.
Parameter: filename – the name of the file to be created. - Side Effects:
- The file is created.
Variables and Expressions¶
- class pulp.LpElement(name)¶
- Base class for LpVariable and LpConstraintVar
- class pulp.LpVariable(name, lowBound=None, upBound=None, cat='Continuous', e=None)¶
This class models an LP Variable with the specified associated parameters
Parameters: - name – The name of the variable used in the output .lp file
- lowbound – The lower bound on this variable’s range. Default is negative infinity
- upBound – The upper bound on this variable’s range. Default is positive infinity
- cat – The category this variable is in, Integer, Binary or Continuous(default)
- e – Used for column based modelling: relates to the variable’s existence in the objective function and constraints
- addVariableToConstraints(e)¶
- adds a variable to the constraints indicated by the LpConstraintVars in e
- classmethod dicts(name, indexs, lowBound=None, upBound=None, cat=0, indexStart=[])¶
Creates a dictionary of LP variables
- This function creates a dictionary of LP Variables with the specified
- associated parameters.
Parameters: - name – The prefix to the name of each LP variable created
- indexs – A list of strings of the keys to the dictionary of LP variables, and the main part of the variable name itself
- lowbound – The lower bound on these variables’ range. Default is negative infinity
- upBound – The upper bound on these variables’ range. Default is positive infinity
- cat – The category these variables are in, Integer or Continuous(default)
Returns: A dictionary of LP Variables
- setInitialValue(val)¶
- sets the initial value of the Variable to val may of may not be supported by the solver
Example:
>>> x = LpVariable('x',lowBound = 0, cat='Continuous')
>>> y = LpVariable('y', upBound = 5, cat='Integer')
gives 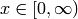 ,
, ![y \in (-\infty, 5]](_images/math/326c558961705f913376f341e986c3cd60159993.png) , an
integer.
, an
integer.
- class pulp.LpAffineExpression(e=None, constant=0, name=None)¶
Bases: pulp.odict.OrderedDict
A linear combination of LpVariables. Can be initialised with the following:
- e = None: an empty Expression
- e = dict: gives an expression with the values being the coefficients of the keys (order of terms is undetermined)
- e = list or generator of 2-tuples: equivalent to dict.items()
- e = LpElement: an expression of length 1 with the coefficient 1
- e = other: the constant is initialised as e
Examples:
>>> f=LpAffineExpression(LpElement('x')) >>> f 1*x + 0 >>> d = LpAffineExpression(dict(x_0=1, x_1=-3, x_2=4)) >>> d 1*x_0 + -3*x_1 + 4*x_2 + 0 >>> x_name = ['x_0', 'x_1', 'x_2'] >>> x = [LpVariable(x_name[i], lowBound = 0, upBound = 10) for i in range(3) ] >>> c = LpAffineExpression([ (x[0],1), (x[1],-3), (x[2],4)]) >>> c 1*x_0 + -3*x_1 + 4*x_2 + 0 >>> c == d 1*x_0 + -3*x_1 + 4*x_2 + -1*x_0 + 3*x_1 + -4*x_2 + 0 = 0 >>> ( c == d) == LpConstraint(0) <class 'pulp.pulp.LpConstraint'>
In brief,
![\textsf{LpAffineExpression([(x[i],a[i]) for i in
I])} = \sum_{i \in I} a_i x_i](_images/math/a65ff68d5d5c7e418ae48024f262dbe3a07083e5.png) where (note the order):
where (note the order):- x[i] is an LpVariable
- a[i] is a numerical coefficient.
- pulp.lpSum(vector)¶
Calculate the sum of a list of linear expressions
Parameter: vector – A list of linear expressions
Constraints¶
- class pulp.LpConstraint(e=None, sense=0, name=None, rhs=None)¶
Bases: pulp.pulp.LpAffineExpression
An LP constraint
Parameters: - e – an instance of LpAffineExpression
- sense – one of LpConstraintEQ, LpConstraintGE, LpConstraintLE (0, 1, -1 respectively)
- name – identifying string
- rhs – numerical value of constraint target
- makeElasticSubProblem(*args, **kwargs)¶
Builds an elastic subproblem by adding variables to a hard constraint
uses FixedElasticSubProblem
Elastic Constraints¶
A constraint 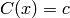 (equality may be replaced by
(equality may be replaced by 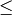 or
or 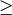 )
can be elasticized to the form
)
can be elasticized to the form
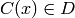
where 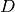 denotes some interval containing the value
denotes some interval containing the value
 .
.
Define the constraint in two steps:
- instantiate constraint (subclass of LpConstraint) with target
.
- call its makeElasticSubProblem() method which returns an object of type FixedElasticSubProblem (subclass of LpProblem) - its objective is the minimization of the distance of
from
.
constraint = LpConstraint(..., rhs = c)
elasticProblem = constraint.makeElasticSubProblem(
penalty = <penalty_value>,
proportionFreeBound = <freebound_value>,
proportionFreeBoundList = <freebound_list_value>,
)
- where:
- <penalty_value> is a real number
- <freebound_value>
![a \in [0,1]](_images/math/5a2448b5338ecf1368d8cb2bdcf47207b7eb2c16.png) specifies a symmetric
target interval
specifies a symmetric
target interval 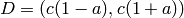 about
about 
- <freebound_list_value> = [a,b], a list of
proportions
![a, b \in [0,1]](_images/math/b2ea940e339aacd33560435120f715e047636d63.png) specifying an asymmetric target
interval
specifying an asymmetric target
interval 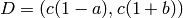 about
about 
The penalty applies to the constraint at points 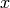 where
where
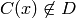 .
The magnitude of <penalty_value> can be assessed by examining
the final objective function in the .lp file written by
LpProblem.writeLP().
.
The magnitude of <penalty_value> can be assessed by examining
the final objective function in the .lp file written by
LpProblem.writeLP().
Example:
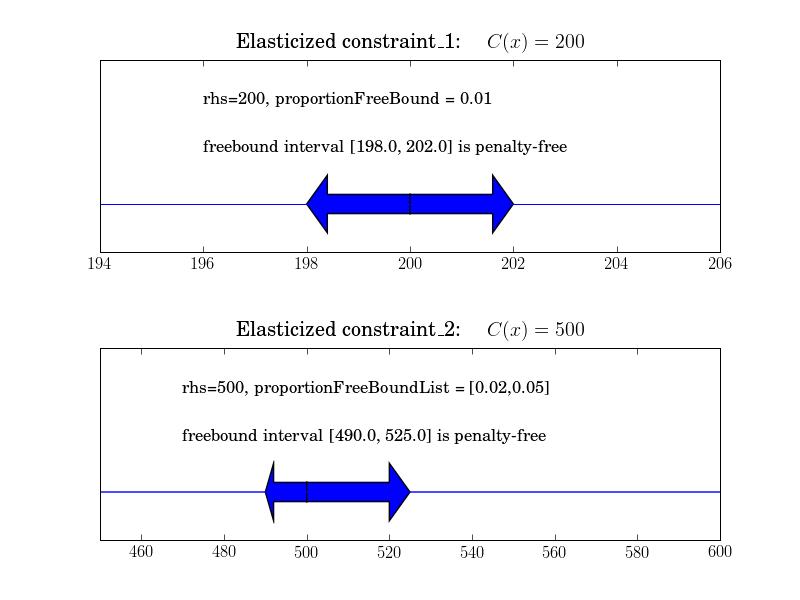
>>> constraint_1 = LpConstraint('ex_1',sense=1,rhs=200)
>>> elasticProblem_1 = constraint_1.makeElasticSubproblem(penalty=1, proportionFreeBound = 0.01)
>>> constraint_2 = LpConstraint('ex_2',sense=0,rhs=500)
>>> elasticProblem_2 = constraint_2.makeElasticSubproblem(penalty=1,
proportionFreeBoundList = [0.02, 0.05])
- constraint_1 has a penalty-free target interval of 1% either side of the rhs value, 200
- constraint_2 has a penalty-free target interval of - 2% on left and 5% on the right side of the rhs value, 500
Following are the methods of the return-value:
- class pulp.FixedElasticSubProblem(constraint, penalty=None, proportionFreeBound=None, proportionFreeBoundList=None)¶
Bases: pulp.pulp.LpProblem
Contains the subproblem generated by converting a fixed constraint
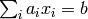 into an elastic constraint.
into an elastic constraint.Parameters: - constraint – The LpConstraint that the elastic constraint is based on
- penalty – penalty applied for violation (+ve or -ve) of the constraints
- proportionFreeBound – the proportional bound (+ve and -ve) on constraint violation that is free from penalty
- proportionFreeBoundList – the proportional bound on constraint violation that is free from penalty, expressed as a list where [-ve, +ve]
- alterName(name)¶
- Alters the name of anonymous parts of the problem
- findDifferenceFromRHS()¶
- The amount the actual value varies from the RHS (sense: LHS - RHS)
- findLHSValue()¶
- finds the LHS value of the constraint (without the free variable and/or penalty variable) - assumes the constant is on the rhs
- isViolated()¶
- returns true if the penalty variables are non-zero
Combinations and Permutations¶
- pulp.combination(orgset, k=None)¶
returns an iterator that lists the combinations of orgset of length k
Parameters: - orgset – the list to be iterated
- k – the cardinality of the subsets
Returns: an iterator of the subsets
example:
>>> c = combination([1,2,3,4],2) >>> for s in c: ... print s (1, 2) (1, 3) (1, 4) (2, 3) (2, 4) (3, 4)
- pulp.allcombinations(orgset, k)¶
returns all permutations of orgset with up to k items
Parameters: - orgset – the list to be iterated
- k – the maxcardinality of the subsets
Returns: an iterator of the subsets
example:
>>> c = allcombinations([1,2,3,4],2) >>> for s in c: ... print s (1,) (2,) (3,) (4,) (1, 2) (1, 3) (1, 4) (2, 3) (2, 4) (3, 4)
- pulp.permutation(orgset, k=None)¶
returns an iterator that lists the permutations of orgset of length k
Parameters: - orgset – the list to be iterated
- k – the cardinality of the subsets
Returns: an iterator of the subsets
example:
>>> c = permutation([1,2,3,4],2) >>> for s in c: ... print s (1, 2) (1, 3) (1, 4) (2, 1) (2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)
- pulp.allpermutations(orgset, k)¶
returns all permutations of orgset with up to k items
Parameters: - orgset – the list to be iterated
- k – the maxcardinality of the subsets
Returns: an iterator of the subsets
example:
>>> c = allpermutations([1,2,3,4],2) >>> for s in c: ... print s (1,) (2,) (3,) (4,) (1, 2) (1, 3) (1, 4) (2, 1) (2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)
- pulp.value(x)¶
- Returns the value of the variable/expression x, or x if it is a number
