|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
| int CppAD::opt_val_hes | ( | const BaseVector & | x, |
| const BaseVector & | y, | ||
| Fun | fun, | ||
| BaseVector & | jac, | ||
| BaseVector & | hes | ||
| ) |
Computing Jabobians and Hessians of Optimal Values.
We are given a function 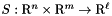 and we define
and we define 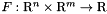 and
and 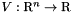 by
by
![\[ \begin{array}{rcl} F(x, y) & = & \sum_{k=0}^{\ell-1} S_k ( x , y) \\ V(x) & = & F [ x , Y(x) ] \\ 0 & = & \partial_y F [x , Y(x) ] \end{array} \]](form_21.png)
We wish to compute the Jacobian and possibly also the Hessian, of 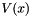 .
.
| BaseVector | The type BaseVector must be a SimpleVector class. We use Base to refer to the type of the elements of BaseVector; i.e., BaseVector::value_type. |
| x | is a vector with size n. It specifies the point at which we evaluating the Jacobian 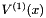 (and possibly the Hessian (and possibly the Hessian 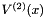 ). ). |
| y | is a vector with size m. It must be equal to 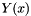 ; i.e., it must solve the implicit equation ; i.e., it must solve the implicit equation
|
| fun | The argument fun is an object of type Fun wich must support the member functions listed below. CppAD will may be recording operations of the type AD<Base> when these member functions are called. These member functions must not stop such a recording; e.g., they must not call AD<Base>::abort_recording. |
Fun::ad_vector must be a SimpleVector class with elements of type AD<Base>; i.e. Fun::ad_vector::value_type is equal to AD<Base>.Fun must support the syntax ell = fun.ell()where
ell is a size_t value that is set to 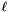 ; i.e., the number of terms in the summation.
; i.e., the number of terms in the summation.Fun must support the syntax s_k = fun.s(k, x, y)The argument
k has prototype size_t k. The argument x has prototype const Fun::ad_vector& x and its size must be equal to n. The argument y has prototype const Fun::ad_vector& y and its size must be equal to m. The return value s_k has prototype AD<Base> s_k and its value must be given by 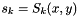 .
.Fun must support the syntax sy_k = fun.sy(k, x, y)The argument
k has prototype size_t k. The argument x has prototype const Fun::ad_vector& x and its size must be equal to n. The argument y has prototype const Fun::ad_vector& y and its size must be equal to m. The return value sy_k has prototype Fun::ad_vector& sy_k, its size is m and its value must be given by 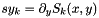 .
.| jac | is a vector with size n or zero. The input values of its elements do not matter. If it has size zero, it is not affected. Otherwise, on output it contains the Jacobian of 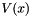 ; i.e., for ; i.e., for  , ,
x is the first argument to opt_val_hes. |
| hes | is a vector with size n * n or zero. The input values of its elements do not matter. If it has size zero, it is not affected. Otherwise, on output it contains the Hessian of 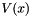 ; i.e., for ; i.e., for  , and , and  , ,
|
hes.size() == 0, the return value is not defined. Otherwise, the return value is the sign of the determinant for 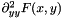 $. If it is zero, then the matrix is singular and
$. If it is zero, then the matrix is singular and hes is not set to its specified value. Definition at line 364 of file opt_val_hes.hpp.