|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
|
CppAD: A C++ Algorithmic Differentiation Package
20171217
|
| void CppAD::local::for_hes_sweep | ( | const local::player< Base > * | play, |
| size_t | n, | ||
| size_t | numvar, | ||
| const Vector_set & | for_jac_sparse, | ||
| const Vector_set & | rev_jac_sparse, | ||
| Vector_set & | for_hes_sparse | ||
| ) |
Given the forward Jacobian sparsity pattern for all the variables, and the reverse Jacobian sparsity pattern for the dependent variables, ForHesSweep computes the Hessian sparsity pattern for all the independent variables.
| Base | this operation sequence was recorded using AD<Base>. |
| Vector_set | is the type used for vectors of sets. It can be either sparse_pack or sparse_list. |
| n | is the number of independent variables on the tape. |
| numvar | is the total number of variables on the tape; i.e., play->num_var_rec(). This is also the number of rows in the entire sparsity pattern for_hes_sparse. |
| play | The information stored in play is a recording of the operations corresponding to a function
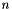 is the number of independent variables and is the number of independent variables and 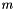 is the number of dependent variables. is the number of dependent variables. |
| for_jac_sparse | For i = 0 , ... , numvar - 1, (for all the variables on the tape), the forward Jacobian sparsity pattern for the variable with index i corresponds to the set with index i in for_jac_sparse. |
| rev_jac_sparse | Input: For i = 0, ... , numvar - 1 the if the function we are computing the Hessian for has a non-zero derivative w.r.t. variable with index i, the set with index i has element zero. Otherwise it has no elements. |
| for_hes_sparse | The forward Hessian sparsity pattern for the variable with index i corresponds to the set with index i in for_hes_sparse. The number of rows in this sparsity patter is n+1 and the row with index zero is not used. Input: For i = 1 , ... , n the forward Hessian sparsity pattern for the variable with index i is empty. Output: For j = 1 , ... , n, the forward Hessian sparsity pattern for the independent dependent variable with index (j-1) is given by the set with index j in for_hes_sparse. |
Definition at line 92 of file for_hes_sweep.hpp.
Referenced by CppAD::ADFun< Base >::for_hes_sparsity(), and CppAD::ADFun< Base >::ForSparseHesCase().