Copyright © 2004 IBM Coportation
Table of Contents
List of Tables
- 2.1. Methods for getting solution information
- 2.2. Some Useful Set and Get Methods
- 2.3. Common Simplex-specific methods
- 2.4. Possible states of a variable
- 4.1. Basic Samples
- 4.2. Advanced Samples
- 4.3. Unsupported Samples
- 4.4. Contents of the Samples directory
- 5.1. Command examples for the clp executable
- 6.1. COIN Messages passed at or above logging level 1
- 6.2. CLP Messages passed at or above logging level 1
- 6.3. COIN Messages passed at or above logging level 0
- 6.4. CLP Messages passed at or above logging level 0
List of Examples
Table of Contents
The COIN Linear Program code or CLP is an open-source simplex solver written in C++. It is primarily meant to be used as a callable library, but a basic, stand-alone executable version is also available.
There are a number of resources available to help new CLP users get started. This document is designed to be used in conjunction with the files in the Samples subdirectory of the main CLP directory (COIN/Clp/Samples). The Samples illustrate how to use CLP and may also serve as useful starting points for user projects. In the rare event that either this document or the available Doxygen content conflicts with the observed behavior of the source code, the comments in the header files, found in COIN/Clp/include, are the ultimate reference.
CLP is written in C++, so it is expected that users of CLP will be writing C++ programs which use CLP as a library. Thus a working knowledge of C++, including basic object-oriented programming terminology is assumed in this document. In addition, the user should be familiar with the fundamental concepts of Linear Programming.
Table of Contents
The basic CLP model class hierarchy is simple. The top three levels of the hierarchy are depicted in the figure below. The first two levels (i.e. ClpModel, ClpSimplex, ClpInterior) contain all the problem data which define a model (that is, a problem instance). The third level contains most of the algorithmic aspects of CLP. There is a fourth level (for models with more general objectives than linear ones), but a description of it is beyond the current scope of this document.
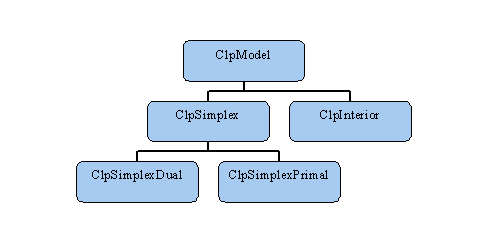
Most Simplex users need only concern themselves with the classes ClpModel and ClpSimplex. There are algorithm-specific classes which inherit from ClpSimplex (e.g. ClpSimplexDual and ClpSimplexPrimal), but they have no member data and rarely need be visible to the user. These classes are cast at algorithm time. So, for example, after instantiating an object model of type ClpSimplex, a user only need call model.dual() to invoke the dual simplex method.
Below is our first CLP sample program. It is short enough to present in full (this code can be found in the CLP Samples directory, see Chapter 4, More Samples ). Most of the remaining examples in this Guide will take the form of small code fragments.
Example 2.1. minimum.cpp
// Copyright (C) 2002, International Business Machines
// Corporation and others. All Rights Reserved.
#include "ClpSimplex.hpp"
int main (int argc, const char *argv[])
{
ClpSimplex model;
int status;
if (argc<2)
status=model.readMps("../../Mps/Sample/p0033.mps");
else
status=model.readMps(argv[1]);
if (!status) {
model.primal();
}
return 0;
}
This sample program creates a ClpSimplex model, reads an MPS file, and if there are no errors, solves it using the primal algorithm. The program is easy to follow, but it is not terribly useful: it does not attempt to inspect the results of the solve. There are two main kinds of results: a "status" describing what happened to the model during the solve, and arrays filled with solution values. Both will be addressed in this chapter.
It is often the case with CLP that there is more than one way to do something. This is a consequence of CLP's mixed heritage as a child of OSL and a cousin of OSI. Finding the status of a model exemplifies this situation.
The OSI way to check for optimality is to call model.isProvenOptimal(). Also available are isProvenPrimalInfeasible(), isProvenDualInfeasible(), isPrimalObjectiveLimitReached(), isDualObjectiveLimitReached(), isIterationLimitReached() or the feared isAbandoned(). Should one prefer the OSL way of doing things, model.status() returns as it would in OSL, so 0 means optimal, 1 means primal infeasible etc.
Similarly, to pick up the solution values, one could inhabit the virtuous world of OSI, or the not-quite-so-virtuous world of OSL and "pure" CLP. By this it is meant that const and non-const forms of arrays are used, respectively. It is easier to deal with the non-const versions, so most of the elaborate algorithms in CLP and its Samples use them.
Table 2.1. Methods for getting solution information
| Purpose | OSI-style (virtuous) | CLP-style (less virtuous) |
|---|---|---|
| Primal column solution | const double * getColSolution() | double * primalColumnSolution() |
| Dual row solution | const double * getRowPrice() | double * dualColumnSolution() |
| Primal row solution | const double * getRowActivity() | double * primalRowSolution() |
| Dual row solution | const double * getReducedCost() | double * dualColumnSolution() |
| Number of rows in model | int getNumRows() | int numberRows() |
| Number of columns in model | int getNumCols() | int numberColumns() |
The reader may have noted a preference for "number" over "num" and "column" over "col". This may be a reaction to when one of the authors was young and 5 or 6 letters was the maximum in FORTRAN for any name or to early days with OSL when seven characters were allowed but the first three had to be "ekk"!
Using the above-listed functions, our initial example might be continued as follows:
Example 2.2. Possible extension of minimum.cpp
int numberRows = model.numberRows();
double * rowPrimal = model.primalRowSolution();
double * rowDual = model.dualRowSolution();
int iRow;
for (iRow=0;iRow<numberRows;iRow++)
printf("Row %d, primal %g, dual %g\n",iRow,
rowPrimal[iRow],rowDual[iRow]);
int numberColumns = model.numberColumns();
double * columnPrimal = model.primalColumnSolution();
double * columnDual = model.dualColumnSolution();
int iColumn;
for (iColumn=0;iColumn<numberColumns;iColumn++)
printf("Column %d, primal %g, dual %g\n",iColumn,
columnPrimal[iColumn],columnDual[iColumn]);
This code sample would pretty-print information about the model's primal and dual solutions. How to additionally print row and column names is illustrated in the defaults.cpp file in the "Samples" directory (the Samples are properly addressed in Chapter 4, More Samples ). This sample is also useful as it explicitly performs default actions (e.g. it sets the primal feasiblility tolerance value to the default value).
The remainder of this chapter will show more of the basic CLP tasks a user might wish to perform. Apart from presolve we will only be looking at actions which can be performed when including the single header file COIN/Clp/include/ClpSimplex.hpp.
Rather than reading a model from an MPS file we can load a model from arrays in memory. There are various loadProblem methods which are similar to those in OSI. It is easy to add more such methods to CLP if the need arises.
We can copy in integer information by copyInIntegerInformation(const char * array) where array is 0 or 1 to say integer and we can drop existing information by deleteIntegerInformation(). There are various ways of changing the size of a model. The simplest is by the use of the method resize(newNumberRows,newNumberColumns) - this will either truncate the model or add "default" rows or columns - a default row has lower bound of -infinity and upper bound of +infinity, while a default column has zero cost, zero lower bound and an upper bound of +infinity.
Normally we would use deleteRows, addRows, deleteColumns and addColumns, where the add methods will also add in the elements. A potentially very useful way of modifying a model is strictly a constructor. Given a large model and a list of rows and a list of columns it constructs the model as a subset of the large model. It is possible to change the order of the columns/rows and to duplicate columns/rows. So a list of columns 4,4,1,0 will create a new model where the first two columns are copies of column 4 in original model and the next two are the first two of original model in reverse order. This can be useful to form a model with piecewise linear costs by duplicating columns and then modifying bounds and costs.
There are set and get methods for tolerances, for example, double primalTolerance() and setPrimalTolerance(double). Assuming that one has a minimization problem, an individual variable is deemed primal feasible if it is less than the tolerance referred to by these methods below its lower bound and less than it above its upper bound. Similarly for dual tolerances, a variable is deemed to be dual feasible if its reduced cost is greater than minus the tolerance or its distance to the upper bound is less than primal tolerance and the reduced cost is less than plus the tolerance or the distance to lower bound is less than primal tolerance. In short, this is complementarity conditions adadpted for tolerances and simple lower and upper bounds.(Note that the above was stated as for minimization; signs are reversed for maximization.)
Table 2.2. Some Useful Set and Get Methods
| Method(s) | Description |
|---|---|
|
setMaximumIterations(int value) int maximumIterations() setMaximumSeconds(double value) double maximumIterations() | These methods tell CLP to stop after a given number of iterations or seconds (and returns these values). |
| double objectiveValue() | This method returns the objective value. |
|
const double * getObjCoefficients() double * objective() | These methods return the objective coefficients. |
|
const double * getRowLower() double * rowLower() const double * getRowUpper() double * rowUpper() const double * getColLower() double * columnLower() const double * getColUpper() double * columnUpper() | These methods give lower and upper bounds on row and column activities. |
|
double * infeasibilityRay() double * unboundedRay() | If the problem was primal or dual infeasible, these methods will give a pointer to a ray proving infeasibility. |
| CoinPackMatrix * matrix() | There are more options as the user has great flexibility in how the problem matrix is stored, but the default matrix class is CoinPackedMatrix (see the section called “Matrix Classes”). So we have that this method returns a pointer to a CoinPackedMatrix which can be further manipulated. |
| CoinBigIndex getNumElements() [a] | Returns the number of elements in the problem matrix. |
|
void setOptimizationDirection(double value) double optimizationDirection() | These methods set and get the objective sense. The parameter value should be +1 to minimize, -1 to maximize, and 0 to ignore. |
[a] CoinBigIndex is a typedef which in most cases is the same as int. | |
Some of the most commonly-used methods when working with Simplex are listed in the table below.
Table 2.3. Common Simplex-specific methods
| Method(s) | Description |
|---|---|
| primal(int mode=0) | This applies the primal algorithm. If mode is set to the default of 0, then the method uses the status variables to determine basis and solution. If mode is 1 then the method does a values pass so variables not in basis are given their current values and one pass of variables is done to clean up the basis with an equal or better objective value. |
| dual(int mode=0) | This applies the dual algorithm. if mode is set to the default of 0, then the method uses the status variables to determine basis and solution. If mode is 1 then the method uses input duals and does a values pass so one pass of basic variables is done to clean up the duals with an equal or better objective value. |
| scaling(int mode=1) | This method toggles scaling on (mode set to 1) and off (mode set to 0). |
| int crash(double gap,int mode) | This method attemps to improve on an all slack basis. For dual this will move variables to the dual feasible bound if the gap between bounds is less than gap. Setting mode to 0 guesses which algorithm is better, while a value of 1 or 2 will result in more work being done. The return code is 0 if the basis was not slacks in first case, it is negative if dual is preferred or positive if primal. ±1 means an all slack basis seemed best, while ±2 means some work was done. |
| perturb(int mode) | This method toggles perturbation on (mode set to 1) and off (mode set to 0). It should be considered a work in progress, although on some problems it gives very good results. |
|
factorizationFrequency() setFactorizationFrequency(int value) | These are "get" and "set" methods for the basis matrix factorization frequency. The default is to refactor every 200 iterations, but it may make more sense to use something such as 100 + the number of rows divided by 50. |
|
dualBound() setDualBound(double value) | These are "get" and "set" methods for the "dual bound". The CLP dual algorithm declares all problems to be dual feasible by putting non-basic variables to correct bounds for the reduced cost. If the gap between the bounds is too big then it pretends the gap is only the value specified by this set method. In essence, this gives a composite dual rather than a pure Phase I- Phase II method. |
|
infeasibilityCost() setInfeasibilityCost(double value) | These are the primal analogs to the "dual bound" methods. |
|
numberPrimalInfeasibilities() sumPrimalInfeasibilities() | After a solve, there may be infeasibilities. These methods serve to check for said infeasibilities. One could check the solution explicitly as well. For a code fragement illustrating this, see Example 2.3, “Presolve code fragment”. |
The header file for the use of CLP's presolve functionality is COIN/Clp/include/Presolve.hpp. The sample program below illustrates some of the possibilities offered by CLP's presolve:
Example 2.3. Presolve code fragment
#include "ClpSimplex.hpp"
#include "ClpPresolve.hpp"
int main (int argc, const char *argv[])
{
ClpSimplex model;
model.readMps("../../Mps/Sample/p0033.mps"); // initialized by readMps or whatever
ClpPresolve presolveInfo;
ClpSimplex * presolvedModel = presolveInfo.presolvedModel(model);
// at this point we have original model and a new model. The information
// on the operations done is in presolveInfo
if (presolvedModel) {
// was not found to be infeasible - so lets solve
// if presolvedModel was NULL then it was primal infeasible and ...
presolvedModel->dual(); // or whatever else we wish to do
presolveInfo.postsolve(true); // the true updates status arrays in original
/* If the presolved model was optimal then so should the
original be.
We can use checkSolution and test feasibility */
model.checkSolution();
if (model.numberDualInfeasibilities()||
model.numberPrimalInfeasibilities())
printf("%g dual %g(%d) Primal %g(%d)\n",
model.objectiveValue(),
model.sumDualInfeasibilities(),
model.numberDualInfeasibilities(),
model.sumPrimalInfeasibilities(),
model.numberPrimalInfeasibilities());
// Due to tolerances we can not guarantee that so you may wish to throw in
model.primal(1);
}
}
Presolve has a few more options which can be found in the header file, for example whether to treat as an integer problem or whether to keep row and column names.
The astute reader may have noticed that the status array has been mentioned once or twice. The beginning user will not need to look at it Nevertheless, for completeness the status of a variable can be found and set as shown below. The possible state of a variable are listed in the following table (each may have to be preceded by ClpSimplex::):
Table 2.4. Possible states of a variable
| Status[a] | Description |
|---|---|
| basic | In basis |
| isFree | Not in basis, has infinite bounds |
| isFixed | Not in basis, bounds are equal |
| atUpperBound | At upper bound, not in basis |
| atLowerBound | At lower bound, not in basis |
| superBasic | Between bounds, but not basic or free |
[a] Status is an enumeration. | |
To get or set the status of a variable is a simple task:
// Get row status... Status status=model.getRowStatus(sequenceNumber) // ... or get column status. Status status=model.getColumnStatus(sequenceNumber) // Set row status to basic (for example)... model.setRowStatus(sequenceNumber,ClpSimplex::basic) // ... or column status to basic. model.setColumnStatus(sequenceNumber,ClpSimplex::basic)
Table of Contents
In the dual algorithm, any infeasible basic variable may be chosen to leave the basis. Similarly in the primal algorithm, any non-basic variable with a "bad" reduced cost may be chosen to enter the basis. This choice is probably the most important factor in determining the number of iterations it will take to solve a problem. Clp provides a abstract base class for each case and then instances of each. It is relatively simple for an advanced user to create new instances.
For the dual method the base class is ClpDualRowPivot. The two existing instances are ClpDualRowDantzig and ClpDualRowSteepest. The Dantzig version implements the "standard" pivot rule: choose the most violated basic variable. It is easily dominated by the Steepest instance which should normally be used. The default is to use un-initialized weights where the initial weight for each basic variable is 1.0. If an all-slack basis is being used then these are the correct weights. To use a version which calculates the weights, create an instance and pass it to ClpSimplex model as in the following code fragment:
ClpDualRowSteepest steep(1); // 0 uninitialized, 1 compute weights model.setDualRowPivotAlgorithm(steep);
Similarly for the primal method the base class is ClpPrimalColumnPivot. The two existing instances are ClpPrimalColumnDantzig and ClpPrimalColumnSteepest. The Dantzig version implements "standard" pivot rule: choose the most "violated" non-basic variable. It is dominated by the Steepest instance which should normally be used. The default is to use exact Devex where the initial weight for each non-basic variable is 1.0. Unlike for the dual, this is never the same as normal steepest edge. To use a version which does steepest edge create an instance and pass it to ClpSimplex model as in the following code fragment:
ClpPrimalColumnSteepest steep(1); // 0 devex, 1 steepest model.setPrimalColumnPivotAlgorithm(steep);
The partial pricing scheme (for long, thin problems) currently does not exist. This could be implemented by anyone who is interested.
The next abstract class of interest is ClpMatrixBase. CLP encapsulates its knowledge of how a matrix is stored in this class. The default instance of this is the ClpPackedMatrix class. This is identical in format to CoinPackedMatrix. Below is a diagram summarizing the hierarchy of the most important matrix classes:
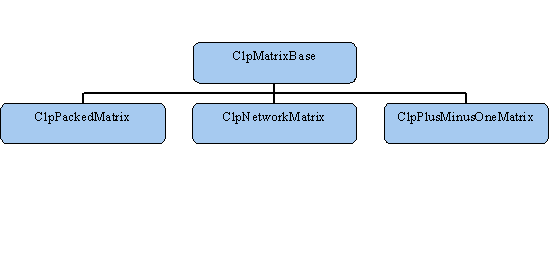
The important new methods implemented are for filling a basis, checking validity of elements and faster "times" and "transposeTimes" when the input array is sparse and/or we have a row copy of the matrix. Advanced users should note that not all methods have to be implemented. In particular, scaling need not be implemented and reverseOrderedCopy can return NULL if a row copy does not make sense.
In addition to the default class, there are two others at present: ClpPlusMinusOneMatrix and ClpNetworkMatrix. As the name implies, the first one is useful when all elements are ±1. In this case multiplies are not needed and more importantly less memory is used and there are fewer cache misses. A class for a matrix where all elements are +1 would be trivial to create. If there were fewer than 64000 rows one could even store row indices as shorts etc.
The use of ClpPlusMinusOneMatrix involves some work as one cannot simply read-in an MPS file. The key is to use loadProblem to pass in a matrix. So if matrix was a CoinPackedMatrix one could do the following:
ClpPlusMinusOneMatrix plusMinus(matrix);
assert (plusMinus.getIndices()); // would be zero if not +- one
model.loadProblem(plusMinus,
lowerColumn,upperColumn,objective,
lower,upper);
ClpNetworkMatrix is similar, but represents a network, thus may only have one element per column. Fortunately, using is is very easy. Given head and tail, one could do the following:
ClpNetworkMatrix network(numberColumns,head,tail);
model.loadProblem(network,
lowerColumn,upperColumn,objective,
lower,upper);
Actual code is in COIN/Clp/Test/unitTest.cpp. A quick glance at the output of this program shows that use of ClpNetworkMatrix gives much faster run times. This is not because of storage issues, but because CLP recognizes the network and uses a network basis factorization which is much faster. However, in this mode CLP is not a genuine network code as it does not take full advantage of the structure by combining operations but it does have the advantage of flexibility.
Other instances are possible. In particular, it should be possible to use the abstract class for column generation or for dynamic matrices which change over time. Minor modifications may be needed but it should work quite smoothly (there is already a dummy "refresh" method which would be used).
Strictly speaking, message handling is a general COIN topic, but it won't hurt to repeat a few important things here.
A simple user you may wish to turn off some output. This is done with model.setLogLevel(int value) where 0 gives nothing and each increase in value switches on more messages. See ClpMessage.cpp, CoinMessage.cpp and Chapter 6, Messages to see which messages are at which level. A more sophisticated user may wish to handle messages in a different way. This is done using passInMessageHandler with a pointer to a handler of the user's own design. The simplest case would be to use the default handler but use a constructor which writes to file. The code would be:
FILE * fp; // assumed open CoinMessageHandler handler(fp); model.passInMessageHandler(&handler);
A still more sophisticated use would be to write a class derived from CoinMessageHandler and then override the print method. Below follows an example which would print only a message for optimality (or infeasibility):
Example 3.1. Sophisticated message handling
class DerivedHandler :
public CoinMessageHandler {
public:
virtual int print() ;
};
int DerivedHandler::print()
{
if (currentSource()=="Clp") {
if (currentMessage().externalNumber()>=0
&& currentMessage().externalNumber()<4) {
// finished
return CoinMessageHandler::print(); // print
}
}
return 0;
}
Table of Contents
The CLP dsitribution includes a number of .cpp sample files. Users are encouraged to use them as starting points for their own CLP projects. The files can be found in the COIN/Clp/Samples/ directory. For the latest information on compiling and running these samples, please see the file COIN/Clp/Samples/INSTALL. Below is a list of some of the most useful sample files with a short description for each file.
Table 4.1. Basic Samples
| Source file | Description |
|---|---|
| minimum.cpp | This is a CLP "Hello, world" program. It reads a problem from an MPS file, and solves the problem. [More...] |
| defaults.cpp | This is one of the simpler driver programs available. It sets tolerances to defaults and is a good place to find straightforward uses of "set" and "get" methods. It also prints out full MPS-like solutions. [More...] |
| driver.cpp | This is designed to be a file that a user could modify to get a useful driver program for his or her project. In particular, it demonstrates the use of CLP's presolve functionality. [More...] |
| network.cpp | This shows the use of non-standard matrices and how to load a problem without the use of MPS files. [More...] |
| testBarrier.cpp | This is a basic driver file for the barrier method of CLP, similar to minimum.cpp. The barrier method is not currently addressed in this guide. [More...] |
Table 4.2. Advanced Samples
| Source file | Description |
|---|---|
| driver2.cpp | This sample, in addition to some tasks common to other samples, does some advanced message handling and presolve. |
| dualCuts.cpp | This sample implements a method of treating a problem as a collection of cuts. |
| decompose.cpp | This does full Dantzig-Wolfe decomposition. It illustrates the use of many models, adding columns, et cetera. |
| sprint.cpp | This solves a long, thin problem by solving smaller subsets. It is a simplified version of work done by one of the authors on aircrew scheduling problems. It shows the use of two models and their synchronization. A more general version can be found in COIN/Clp/ClpSolve.cpp |
| sprint2.cpp | This is similar to sprint.cpp but is designed for solving large problems with little choice. The idea is that if relatively few variables are fixed, presolve can greatly reduce the problem size so that a series of solves can get close to the optimal solution much faster than would a naďve solve of the full problem. |
The remaining Samples listed here are considered unsupported in that they are of a more esoteric nature and are sometimes contributed as a result of an individual's request. The are to be found in COIN/Clp/Samples/Contributed.
Table 4.3. Unsupported Samples
| Source file | Description |
|---|---|
| testBasis.cpp | This sample takes a problem, changes any inequality constraints to equality constraints, solves the problem, and creates the optimal basis. |
| testGub.cpp | This sample illustrates the use of the GUB ("Generalized Upper Bound") technique. |
| ekk.cpp | This sample can be used to compare CLP and OSL. It uses an additional file in the Samples directory, ekk_interface.cpp. These sample files are not likely to be interesting to new CLP users who do not have experience with OSL. |
| hello.cpp | This sample creates a text-based picture of a matrix on screen (limited to an 80x80 matrix). It's not terribly useful but it does illustrate one way to step through the elements of a matrix. |
| piece.cpp | This sample takes a matrix read in by CoinMpsIo (can be used to read in MPS files without a solver), deletes every second column and solves the resulting problem. |
| useVolume.cpp | The Volume Algorithm is another solver available as part of the COIN-OR distribution. This sample shows how to use the Volume Algorithm with CLP. |
This sample is examined in more detail in the section called “ First Example ”.
This sample begins by reading an MPS file. The default MPS file is COIN/Mps/Sample/p0033.mps; this can be over-riden by a command-line specification of a (path and) file name). The sample then sets the pivot algorithm to be exact devex. It "gets" the default infeasibility cost and "sets" it to that value (and prints it to standard out). This sort of getting and setting of various parameters constitutes a common theme in this sample, with the purpose of illustrating usage of some of the more common get and set methods available in CLP.
At this point the model is solved by the primal method. A sequence of sets, gets and prints is then followed by a number of calls to methods which give specific information about the status of the problem (for example, the code checks that the current solution has been proven to be optimal by assert(model.isProvenOptimal())).
Next, a copy of the original model is made. More sets and gets are performed to demonstrate the use of additional options (including the setting of the default message handling as well as changing of the "log level" (amount of output)). The model is solved again a number of times between changes of the optimization direction (i.e. changing from min to max or vice versa). The remaining lines of this sample serve to display solution and problem information in much the same way as is done in driver.cpp.
This sample begins by reading an MPS file. The default MPS file is COIN/Mps/Sample/p0033.mps; this can be over-riden by a command-line specification of a (path and) file name). A second command-line argument can specify that either the "primal" or "dual" method (or even the "barrier", see below) should be used by CLP.
Once the problem has been read, there are two options for how to solve it, one of which must be chosen at compile-time (STYLE1 being defined or not determines this choice). The second manner is more flexible and involves more specific directions being given to CLP, including the ability to specify that the barrier method should be used.
At this point in the sample, the problem is solved by CLP, and some basic ouput is generated. If more output is desired, at compile-time, an exit(0) statement must either be removed or commented. There are two levels of additional output, the first of which is suppressed by a #if 0 directive which may be modified at compile-time if desired. This first level of output only involves non-zero columns, whereas the second provides additional information.
This handy sample reads a network problem generated by netgen, converts it to an LP using CLP's network matrix type, and solves. This entirely avoids the use of an MPS file, as the LP is built in memory from the network data file created by netgen. Also, the factorization frequency is changed, and the problem is solved more than once (demonstrating the change of optimization sense as well as switching from dual to primal methods).
This straightfoward sample begins by reading a problem from an MPS file. It then chooses a Cholesky factorization and solves the problem using the predictor corrector barrier method. It then copies the problem and performs a crossover to a simplex solution in the new copy.
This sample begins with only the equality constraints of a problem. The inequalities are considered to be part of a pool of available cuts in much the same way as is done in integer programming. However, in this case, the cuts are not "generated", they are simply the inequalities of the problem.
Below is a listing of a number of common CLP tasks, such as loading a problem from an MPS file, matched with a list of each Sample file which illustrates the performance of a given task.
Table 4.4. Contents of the Samples directory
| CLP Task(s) | Method(s) | Sample(s) |
|---|---|---|
| Read problem from MPS file |
int readMps(const char *filename) | defaults.cpp, driver.cpp, minimum.cpp |
| Solve by primal method |
int primal() | driver.cpp |
| Choose pivot rule |
void setPrimalColumnPivotAlgorithm(ClpPrimalColumnPivot &choice) | defaults.cpp |
| Get/set infeasibility cost |
void setInfeasibilityCost(double value) | defaults.cpp |
| Get string/"double"/integer information |
bool getStrParam(ClpStrParam key, std::string &value) const | defaults.cpp |
| Set maximum number of iterations |
void setMaximumIterations(int value) | defaults.cpp |
| Check solution status |
int status() const | |
Table of Contents
The result of make unitTest (executed in COIN/Clp) is an executable clp as well as the CLP and COIN libraries. The executable can be used to perform various unit tests, but can also be used as a standalone solver. As the executable has a very simple solution file format, the user may wish to modify COIN/Clp/Test/ClpMain.cpp, which contains the source of the executable (modifications could even be offered as a contribution to CLP).
The clp executable operates in command line mode or prompted mode. Entering clp will invoke the prompted mode, while clp <filename> will import a problem in MPS format from filename, solve it using the dual simplex method and exit. The command clp <filename> -primalsimplex instructs the executable tp import a file and solve using the primal simplex method. An additional solitary dash ("-") starts the prompt mode once the execution of the initial command has been completed. The "-" is necessary as part of the command; invoking prompt mode as a separate command will result in the loss of problem information related to the initial command. So, the following sequences of commands are equivalent in the sense that both maximize a problem using the dual simplex method and write a solution to file: solfile:
$ clp filename -maximize -dualsimplex -solution solfile
$ clp filename -maximize -
Clp:duals
Clp:solution solfile
Clp:quit
The executable is at a very early stage of development. Comments and suggestions would be appreciated.
The executable has some command-completion functionality as well as some online help. Below is a table with some examples which summarize these capabilities.
Table 5.1. Command examples for the clp executable
| Command | Result |
|---|---|
| ? | Gives a list of all commands |
| p? | Gives a list of all commands which begin with <p>. |
| p?? | Gives a list of all commands which begin with <p>., with a short explanation for each. |
| primals?? | If is this is enough to uniquely determine a command (in this example, primalS, for primal simplex), a long explanation is given. |
In addition, matching a name without a ? will either execute the command or give the value of the corresponding parameter as follows: primalw will give the current value of the primalWeight parameter while primalw 1.0e7 will change it to 1.0e7.
Below is a sample CLP executable prompt-mode session. A small problem is loaded and solved under various conditions with the primal and dual simplex methods. Note the use of the allslack command; it sets the basis to all slacks and resets the solution.
$clp
Coin LP version 0.99.9, build Sep 14 2004
Clp takes input from arguments ( - switches to stdin)
Enter ? for list of commands or help
Clp:import../Mps/Sample/p0033.mps
At line 15 NAME P0033
At line 16 ROWS
At line 34 COLUMNS
At line 109 RHS
At line 118 BOUNDS
At line 152 ENDATA
Problem P0033 has 16 rows, 33 columns and 98 elements
Model was imported from ./../Mps/Sample/p0033.mps in 0 seconds
Clp:primals
Presolve 15 (-1) rows, 32 (-1) columns and 97 (-1) elements
0 Obj 0 Primal inf 27.2175 (10) Dual inf 6.42094e+11 (32)
32 Obj 2520.57
Optimal - objective value 2520.57
After Postsolve, objective 2520.57, infeasibilities - dual 0 (0), primal 0 (0)
Optimal objective 2520.571739 - 32 iterations time 0.012, Presolve 0.01
Clp:max
Clp:primals
Presolve 11 (-5) rows, 25 (-8) columns and 84 (-14) elements
0 Obj 4807.92 Dual inf 1700.71 (15)
End of values pass after 2 iterations
2 Obj 4921.7 Dual inf 580.637 (5)
9 Obj 5299.7
Optimal - objective value 5299.7
After Postsolve, objective 5299.7, infeasibilities - dual 643.608 (9), primal 27.0826 (10)
Presolved model was optimal, full model needs cleaning up
0 Obj 5299.7
0 Obj 5299.7
Optimal - objective value 5299.7
Optimal objective 5299.698868 - 9 iterations time 0.022, Presolve 0.02
Clp:allslack
Clp:duals
Presolve 11 (-5) rows, 25 (-8) columns and 84 (-14) elements
0 Obj 2752 Primal inf 24.4867 (6) Dual inf 4280.55 (25)
8 Obj 5299.7
Optimal - objective value 5299.7
After Postsolve, objective 5299.7, infeasibilities - dual 704.58 (8), primal 27.0792 (10)
Presolved model was optimal, full model needs cleaning up
0 Obj 5299.7
0 Obj 5299.7
Optimal - objective value 5299.7
Optimal objective 5299.698868 - 8 iterations time 0.032, Presolve 0.01
Clp:min
Clp:duals
Presolve 15 (-1) rows, 32 (-1) columns and 97 (-1) elements
0 Obj 5299.7 Dual inf 4632.26 (28)
16 Obj 2520.57
Optimal - objective value 2520.57
After Postsolve, objective 2520.57, infeasibilities - dual 2052.5 (13), primal 27.1143 (10)
Presolved model was optimal, full model needs cleaning up
0 Obj 2520.57
0 Obj 2520.57
Optimal - objective value 2520.57
Optimal objective 2520.571739 - 16 iterations time 0.012, Presolve 0.01
Clp:allslack
Clp:presolve off
Clp:primals
0 Obj 0 Primal inf 27.2175 (10) Dual inf 6.39167e+11 (32)
32 Obj 2520.57
Optimal - objective value 2520.57
Optimal objective 2520.571739 - 32 iterations time 0.002
Clp:allslack
Clp:maxIt 10
maxIterations was changed from 99999999 to 10
Clp:primals
0 Obj 0 Primal inf 27.2175 (10) Dual inf 6.39167e+11 (32)
Stopped - objective value 4.24664e+10
Stopped objective 4.246637759e+10 - 10 iterations time 0.002
Clp:quit
Some of the more common messages and codes passed by CLP are listed in the tables below. This is list is not meant to exhaustive. The notation is as for printf from "C":
- %s is a string
- %d is an integer
- %g or %f is a floating point value
Table 6.1. COIN Messages passed at or above logging level 1
| Code | Area | Text and notes | |
|---|---|---|---|
| 1 | MPSREAD | At line %d %s | |
|
This just prints out NAME line, ROW line, etc | |||
| 2 | MPSREAD | Problem %s has %d rows, %d columns and %d elements | |
|
This gives statistics after reading an MPS file | |||
| 8 | MPSREAD | %s read with %d errors | |
|
This gives error statistics for file | |||
| 505 | PRESOLVE | Presolved poblem not optimal, resolve after postsolve | |
|
This could be because it was not feasible or because of maximum iterations. If this message occurs then consider using primal clean up | |||
| 506 | PRESOLVE | Presolve %d (%d) rows, %d (%d) columns and %d (%d) elements | |
|
The first number is the number after presolve and the number in parentheses is amount of reduction | |||
| 510 | PRESOLVE | Presolve is modifying %d integer bounds and re-presolving | |
|
If presolve determines at the end that an integer variable have its bounds changed then it will repeat the entrire presolve | |||
| 511 | PRESOLVE | After Postsolve, objective %g, infeasibilities - dual %g (%d), primal %g (%d) | |
|
This gives the state after postsolve - this gives the objective value and the sum of dual and primal infeasibilities with the number of infeasibilities in parentheses. Hopefully these should be zero | |||
| 512 | PRESOLVE | Presolved model was optimal, full model needs cleaning up | |
|
If the numbers in previous message (511) were large then maybe we need to know, if small then that's life | |||
Table 6.2. CLP Messages passed at or above logging level 1
| Code | Area | Text and notes | |
|---|---|---|---|
| 1 | SIMPLEX | Primal infeasible - objective value %g | |
|
You may need to look at previous messages or use methods. Such as sumPrimalInfeasibilities() to find cause | |||
| 2 | SIMPLEX | Dual infeasible - objective value %g | |
|
You may need to look at previous messages or use methods. Such as sumDualInfeasibilities() to find cause | |||
| 3 | SIMPLEX | Stopped - objective value %g | |
|
The algorithm stopped as requested by the user. | |||
| 4 | SIMPLEX | Stopped due to errors - objective value %g | |
|
Switch on log level 2 to see information on size of elements etc. If they look reasonable then maybe we need to know. | |||
| 5 | SIMPLEX | %d Obj %g Primal inf %g (%d) Dual inf %g (%d) | |
|
At each re-factorization this gives the number of iterations and the value of the objective function. If there are primal infeasibilities then the sum and number are given and similarly for dual infeasibilities. (This is a simplified form of message.) | |||
| 14 | SIMPLEX | Perturbing problem by %g % of %g | |
|
There is more to this message but if the user sees this then s/he has chosen to perturb the problem or the algorithm has decided to do so. If the numbers look too large the user may wish to think again. | |||
| 19 | SIMPLEX | %d variables/rows fixed as scaled bounds too close | |
|
If this occurs look carefully at your input data | |||
| 24 | SIMPLEX | Matrix will be packed to eliminate small elements | |
|
If this occurs the user should look carefully at data. | |||
| 26 | SIMPLEX | Matrix will be packed to eliminate %d duplicate elements | |
|
If this occurs the user should look carefully at data. | |||
| 28 | SIMPLEX | Crash put %d variables in basis, %d dual infeasibilities | |
|
| |||
| 29 | SIMPLEX | End of values pass after %d iterations | |
|
??? If primal(1) or dual(1) the a sweep through model is made and this signals end of pass. | |||
Table 6.3. COIN Messages passed at or above logging level 0
| Code | Area | Text and notes | |
|---|---|---|---|
| 3001 | MPSREAD | Illegal value for %s of %g | |
|
String will be "infinity" if setInfinity passed bad value, or "default integer bound" if setDefaultBound passed bad value. | |||
| 3002 | MPSREAD | Bad image at line %d < %s > | |
|
This gives line number and the offending line | |||
| 3003 | MPSREAD | Duplicate objective at line %d < %s > | |
|
An objective row appears twice in one column | |||
| 3004 | MPSREAD | Duplicate row %s at line %d %s | |
|
The named row appears twice in one column. | |||
| 3005 | MPSREAD | No match for row %s at line %d < %s > | |
|
The named row did not appear in ROWS section. | |||
| 3006 | MPSREAD | No match for column at line %d < %s > | |
|
The named column (in BOUNDS section) did not appear in COLUMNS section. | |||
| 6001 | MPSREAD | Unable to open mps input file %s | |
|
| |||
| 6002 | MPSREAD | Unknown image %s at line %d of file %s | |
|
The Mps reader could not make sense of the image file specified. | |||
| 6003 | MPSREAD | Consider the possibility of a compressed file which zlib is unable to read. | |
|
Some .gz files can not be read by zlib. Using gunzip and then gzip normally cures problem. | |||
| 6004 | MPSREAD | EOF on file %s | |
|
The Mps reader did not find expected section marker. | |||
| 6005 | MPSREAD | Returning as too many errors | |
|
The reader has put out 100 messages and is giving up. | |||
| 507 | PRESOLVE | Presolve determined that the problem is infeasible with tolerance of %g | |
|
If you want you can try with a larger tolerance | |||
| 508 | PRESOLVE | Presolve thinks problem is unbounded | |
|
Perhaps the user should maximize if initially minimizing or vice versa. | |||
| 509 | PRESOLVE | Presolve thinks problem is infeasible AND unbounded??? | |
|
If you get this message we want to know | |||
Table 6.4. CLP Messages passed at or above logging level 0
| Code | Area | Text and notes | |
|---|---|---|---|
| 3002 | SIMPLEX | Not solving empty problem - %d rows, %d columns and %d elements | |
|
Test problem size before solving. | |||
| 6002 | SIMPLEX | %d bad bound pairs or bad objectives were found | |
|
Either the value in the objective was too large or a lower bound was greater than an upper bound. | |||
| 6003 | SIMPLEX | Matrix has %d large values, first at column %d, row %d is %g | |
|
Some of the values in matrix are ridiculous. | |||
| 6004 | SIMPLEX | Can't get out of loop ... | |
|
| |||
There are also messages available at log level 2 (the most likely useful relate to scaling), and will be addressed in a future version of this User Guide.
- Q: What is CLP?
- Q: What are some of the features of CLP?
- Q: How do I obtain and install CLP?
- Q: Is CLP reliable?
- Q: On which platforms does CLP run?
- Q: Is there any documentation for CLP?
- Q: Is CLP as fast as OSL?
- Q: When will version 1.0 of CLP be available?
- Q: The barrier method sounds interesting, what are some of the details?
- Q: Which Cholesky factorizations codes are supported by CLP's barrier method?
- Q: When will CLP have a good native ordering?
- Q: Is the barrier code as mature as the simplex code?
- Q: Which algorithm should I use for quadratic programming and should I keep an eye open for any issues?
- Q: What can the community do to help?
| Q: | What is CLP? |
| A: | (DN 08/27/04) The COIN-OR LP code is designed to be a high quality Simplex code provided under the terms of the Common Public License. CLP is written in C++, and is primarily intended to be used as a callable library (though a rudimentary stand-alone executable exists). The first release was version .90. The current release is version .99.9. |
| Q: | What are some of the features of CLP? |
| A: | (DN 08/27/04) CLP includes primal and dual Simplex solvers. Both dual and primal algorithms can use matrix storage methods provided by the user (0-1 and network matrices are already supported in addition to the default sparse matrix). The dual algorithm has Dantzig and Steepest edge row pivot choices; new ones may be provided by the user. The same is true for the column pivot choice of the primal algorithm. The primal can also use a non linear cost which should work for piecewise linear convex functions. CLP also includes a barrier method for solving LPs. |
| Q: | How do I obtain and install CLP? |
| A: | (DN 08/27/04) Please see the COIN-OR FAQ for details on how to obtain and install COIN-OR modules. |
| Q: | Is CLP reliable? |
| A: | (DN 09/07/04) CLP has been tested on many problems of up to 1.5 million constraints and has shown itself as reliable as OSL. It is also being tested in the context of SBB ("Simple Branch and Bound", which is used to solve integer programs), but more testing is needed before it can get to version 1.0. SBB has been replaced by Cbc. |
| Q: | On which platforms does CLP run? |
| A: | (DN 08/27/04) CLP compiles and has been tested (to varying degrees) on the following platforms:
|
| Q: | Is there any documentation for CLP? |
| A: | (DN 09/16/04) An early release of a User Guide is available on the CLP documentation webpage. Also available is a list of CLP class descriptions generated by Doxygen. |
| Q: | Is CLP as fast as OSL? |
| A: | (DN 08/27/04) CLP uses sparse matrix techniques designed for very large problems. The design criteria were for it not to be too slow. Some speed has been sacrificed to make the code less opaque OSL (not difficult!). |
| Q: | When will version 1.0 of CLP be available? |
| A: | (DN 08/27/04) It is expected that version 1.0 will be released in time for the 2004 INFORMS Annual Meeting (24-27 October, 2004). |
| Q: | The barrier method sounds interesting, what are some of the details? |
| A: | (DN 08/30/04) The CLP barrier method solves convex QPs as well as LPs. In general, a barrier method requires implementation of the algorithm, as well as a fast Cholesky factorization. CLP provides the algorithm, and is expected to have a reasonable factorization implementation by the release of CLP version 1.0. However, the sparse factorization requires a good ordering algorithm, which the user is expected to provide (perhaps a better factorization code as well). |
| Q: | Which Cholesky factorizations codes are supported by CLP's barrier method? |
| A: | (DN 09/16/04) The Cholesky interface is flexible enough so that a variety of Cholesky ordering and factorization codes can be used. Interfaces are provided to each of the following:
|
| Q: | When will CLP have a good native ordering? |
| A: | (DN 09/16/04) The best outcome would be to have an existing ordering code available as part of the COIN distribution under the CPL. However, if this is not possible, the native ordering will be made respectable. |
| Q: | Is the barrier code as mature as the simplex code? |
| A: | (DN 09/16/04) The simplex code has been exposed to user testing for more than a year and and the principal author, John Forrest, knows more about simplex algorithms than interior point algorithms, so the answer is "no". However, it performs well on test sets and seems to be more reliable than some commercially available codes (including OSL). |
| Q: | Which algorithm should I use for quadratic programming and should I keep an eye open for any issues? |
| A: | (DN 09/16/04) The interior point algorithm for quadratic programming is much more elegant and normally much faster than the quadratic simplex code. Caution is suggested with the presolve as not all bugs have been found and squashed when a quadratic objective is used. One may wish to switch off the crossover to a basic feasible solution as the simplex code can be slow. The sequential linear code is useful as a "crash" to the simplex code; its convergence is poor but, say, 100 iterations could set up the problem well for the simplex code. |
| Q: | What can the community do to help? |
| A: | (DN 09/09/04) A lot! A good first step would be to join the CLP mailing lists. Some other possibilities:
|
There is Doxygen content for CLP available online at http://www.coin-or.org/Doxygen/Clp/index.html. A local version of the Doxygen content can be generated from the CLP distribution. To do so, in the directory COIN/Clp, enter make doc. The Doxygen content will be created in the directory COIN/Clp/Doc/html. The same can be done for the COIN core, from the COIN/Coin directory.
| Revision History | ||
|---|---|---|
| Revision 0.4 | 18 Oct 2004 | DdlN |
| Second official release, including some corrections, clarifications, and several improvements (better treatment of clp executable and Samples). | ||
| Revision 0.3 | 19 Aug 2004 | DdlN |
| Major overhaul, including transition from MS Word to DocBook XML. | ||
| Revision 0.2 | 23 Feb 2004 | RLH |
| Revisions to make it clearer to the non-author reader. | ||
| Revision 0.1 | Nov 2003 | JF |
| First draft | ||